Contacts
Giulia Meuli, PhD student ([email protected])
Mathias Soeken, Post-Doc ([email protected])
Giovanni De Micheli, Professor ([email protected])
Motivation
Unique physic properties give quantum computers the ability to solve computational problems faster than their classical counterparts. There is a worldwide effort to build the first practical quantum computer and many companies are betting on different technologies. This is one of the few fields where research on physical devices is moving from academia to companies: Microsoft, Google, IBM, Intel, as well as the rapidly growing startup companies IonQ and Rigetti, are investing significant effort into building the first scalable quantum computer. They are all looking forward to reach quantum advantage, which is the ability to solve problems that cannot be solved classically.
According to many companies, practical systems will soon be available but will have significant hardware constraints, particularly a limited number of qubits. Existing manual methods for the synthesis of quantum circuits are not scalable and may not be able to meet hardware constraints. In this unlucky scenario we will have a practical quantum computer not being able to use it. This research is capable of enabling quantum algorithms to be run on constrained systems, providing efficient automatic tools for quantum compilation.
Goals
The final goal of my PhD research is to develop automatic tools to empower quantum algorithm designers with the support that is provided to digital designers by commercial EDA tools. I study how classical logic synthesis methods can be adapted to perform in the context of quantum computing. A main challenge is given by the constant changing of the technology constraints, in terms of number of available qubits and quantum operation accuracy. Another challenge and main difference from classical systems is that quantum computers only support reversible operations, so requiring reversible logic synthesis methods. I mainly focus on synthesis and optimization of quantum circuits.
Research highlights
The best-fit mapping method
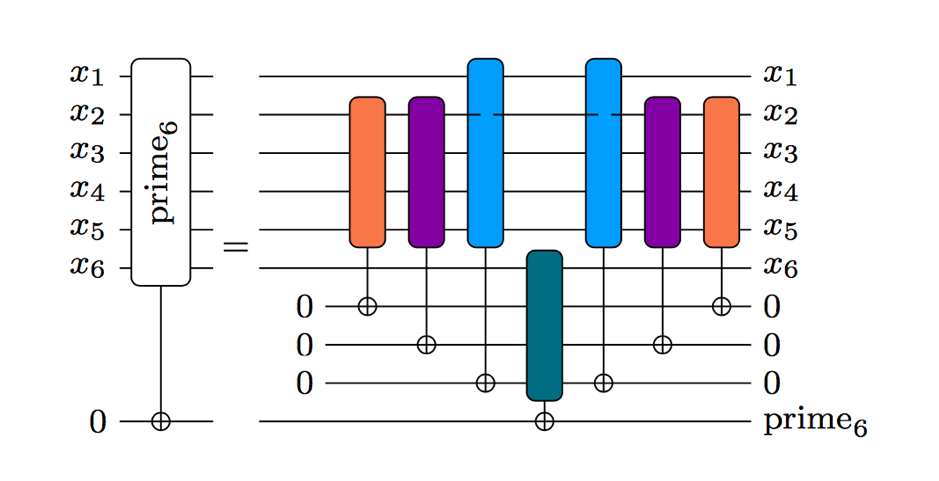
The developed method addresses the problem of translating single-target gates (reversible gate) into quantum circuits. Given a cascade of single-target gates representing a Boolean function to be synthesized, a possible strategy is to apply ESOP-based decomposition (a technique is capable of performing the mapping without using extra ancillae). Nevertheless, this method is not scalable, since extracting a two-level expression for function with large number of inputs is a complex operation.
We propose an LUT-based mapping method, that is scalable and capable of taking the best advantage from extra ancillae that are often available, to reduce the T-count (number of expensive T gates). This technique exploits LUT mapping to translate a single-target gate into a network of multiple-controlled Toffoli gates.
Post-synthesis optimization of reversible circuits
We formalized some rules for post-synthesis optimization of Toffoli networks, aiming at reducing the T-count of the synthesized quantum circuit. We use maximum weighted graph matching to find an optimal optimization strategy. The optimization is effective for reversible circuits obtained with ESOP-decomposition; since these circuits consist of a set of multiple-controlled Toffoli gates all acting on the same target lines.
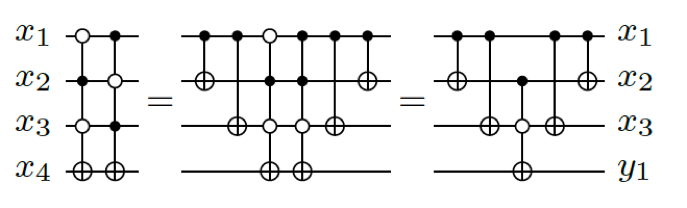
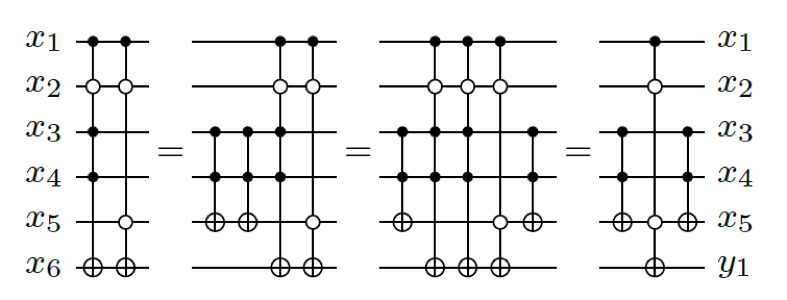
Minimisation of the number of CNOT gates using SAT
As the quantum technology processes are not yet standardized, the cost functions are always changing with the technology development. An important parameter to be minimized is the bare number of gates, since even more elementary gates as the CNOT seem now to have an impact on the quality of the computation. In fact, 2-qubit gates typically have a worse fidelity and higher gate error rate.
We developed a method that minimizes the number of CNOT gates in a Clifford+T circuit by using a SAT-based exact algorithm to synthesize minimum {CNOT, T} circuits.
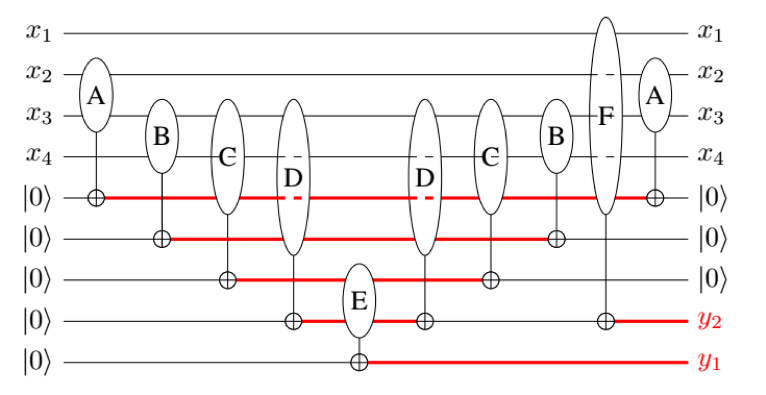
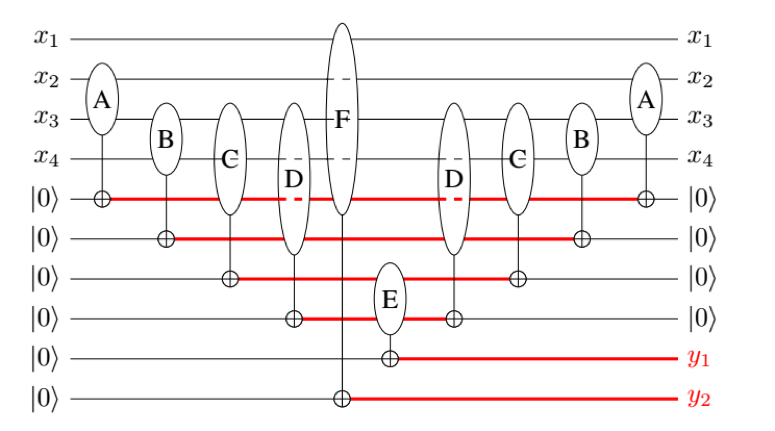
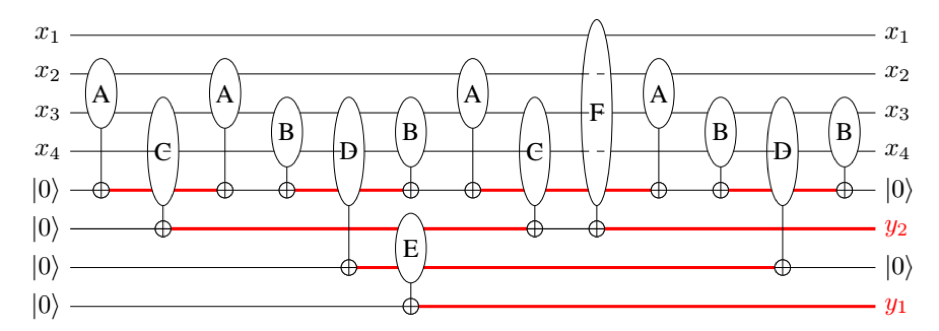
Quantum memory management
Quantum memory management is becoming a pressing problem, especially given the recent research effort to develop new and more complex quantum algorithms. The only existing automatic method for quantum states clean-up relies on the availability of many extra resources.
We propose an automatic tool for quantum memory management. We show how this problem exactly matches the reversible pebbling game. Based on that, we develop a SAT-based algorithm that returns a valid clean-up strategy, taking the limitations of the quantum hardware into account. The developed tool empowers the designer with the flexibility required to explore the trade-off between memory resources and number of operations.