The latest version of the EPFL combinational benchmarks can be found on GitHub.
Introduction:
The EDA community heavily relies on public benchmarks to evaluate the performance of academic and commercial design tools. Logic optimization and synthesis are core EDA applications where benchmarking is essential to develop effective methodologies.
With the aim of defining a new comparative standard for the logic optimization and synthesis community, we introduce the The EPFL Combinational Benchmark Suite. It consists of 23 natively combinational circuits designed to challenge modern logic optimization tools. The benchmark suite is divided into arithmetic, random/control and MtM parts.
Each circuit is distributed in Verilog, VHDL, BLIF and AIGER formats.
Download the EPFL benchmark suite, optimize it and send us your improved LUT-6 implementation! The best results will be published online together with authors’ names and affiliations!
Arithmetic Benchmarks:
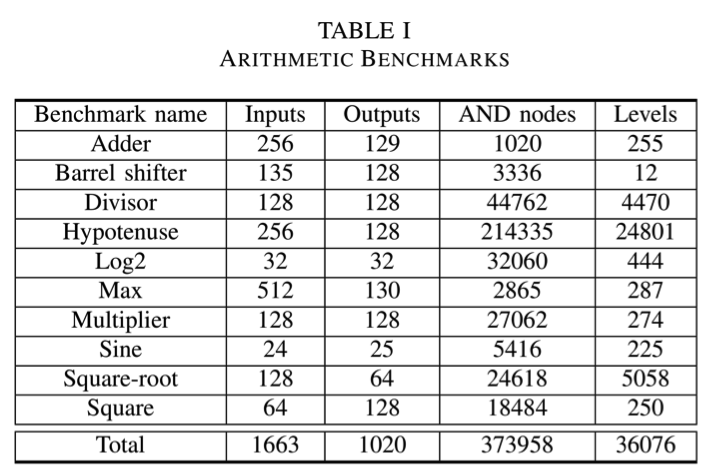
This part consists of 10 arithmetic benchmarks, e.g., square-root, hypotenuse, divisor, multiplier etc. They are obtained by a simple-minded (automated) mapping of arithmetic computational algorithms into basic logic gates. The initial implementations are intendedly sub-optimal to test the ability of optimization tools. The arithmetic benchmarks come in different bit-widths to provide diversity in the implementation complexity. Table I shows their initial characteristics in terms of And/Inverter Graph (AIG) representation. In total, the arithmetic benchmarks count about 0.37M nodes and 36k levels.
Random/Control Benchmarks:
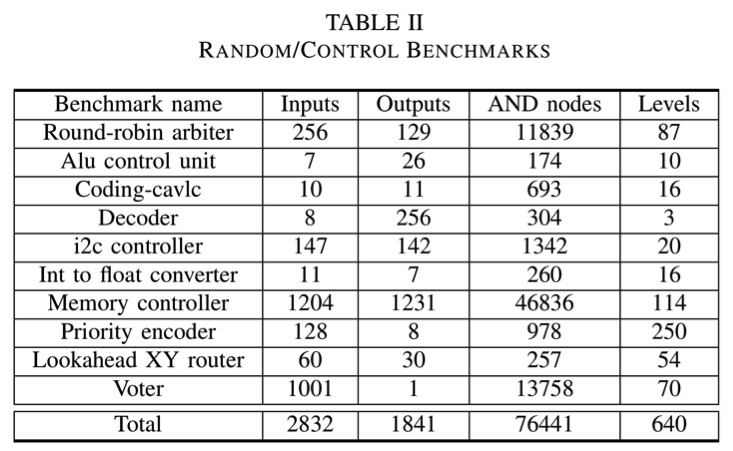
The set of random/control benchmarks in the EPFL suite consists of various types of controllers, arbiters, routers, converters, decoders, voters and random functions. It contains 10 circuits mapped into simple gates from behavioral descriptions. Table II shows their initial characteristics in terms of and/inverter graph (AIG) representation. Also here, the initial implementations are intendedly unoptimized. In total, the random/control benchmarks count about 76k nodes and 0.6k levels.
More than ten Million gates (MtM) Benchmarks:
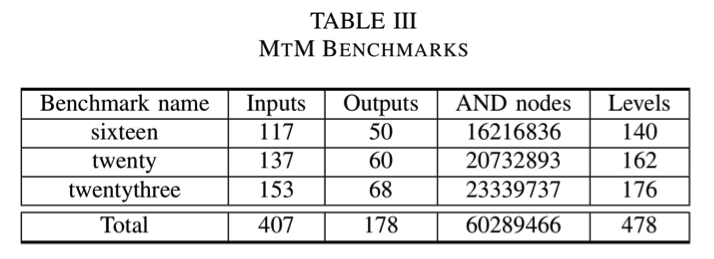
The More than ten Million gates (MtM) benchmarks are designed to challenge the size capacity of modern optimization tools. In the EPFL combinational benchmark suite there are three of such MtM circuits. They are extracted from a set of random Boolean functions, generated with a custom computer program, using as selection metric the implementation complexity. Table II shows their characteristics in terms of and/inverter graph (AIG) representation. In total, the MtM benchmarks count about 60M nodes and 4.8k levels.
LUT-6 Mapping:
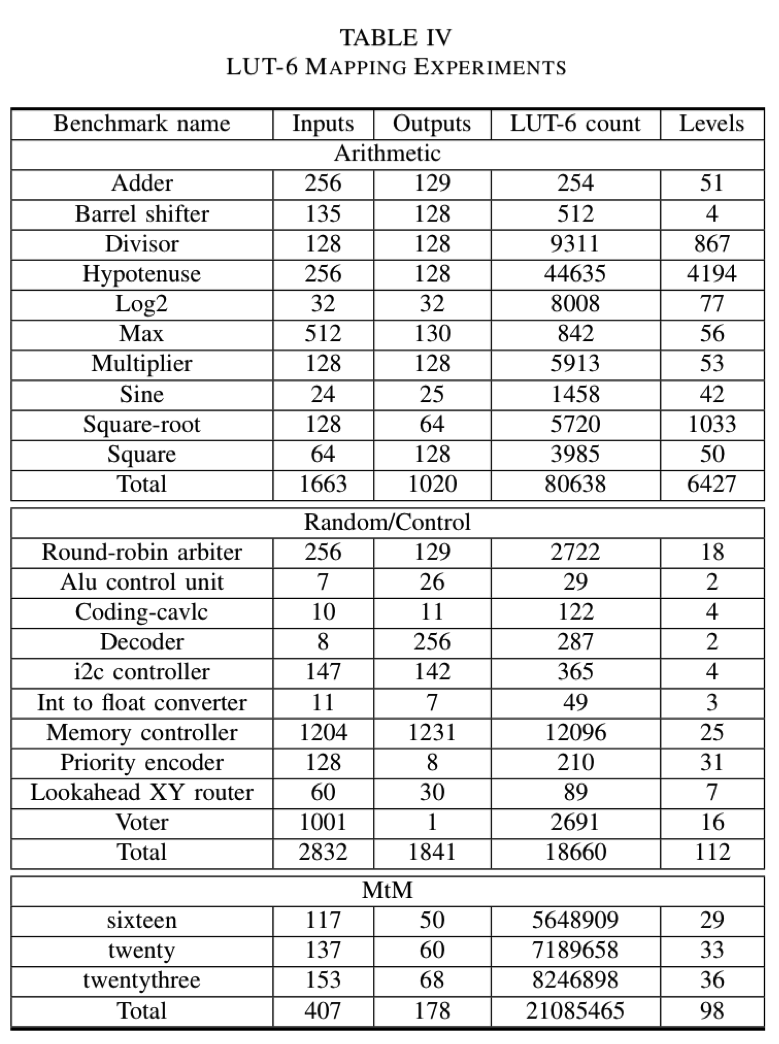
Table IV shows LUT-6 mapping experiments for the EPFL combinational benchmark suite. They are performed using ABC academic tool [2], with the pure mapping command if -K 6.
Best LUT-6 Implementations:
The latest best synthesis results can be found in the releases of the GitHub repository.
Submit your best LUT-6 implementation!
We keep track of the best optimization results, mapped into LUT-6, for size and depth metrics. We encourage researchers to submit their best LUT-6 implementations in BLIF format for one or more of the benchmarks by making a pull request on GitHub or sending an email to [email protected] (in case the files exceed 3 MB please provide a download link in the email). Also the methodology used to optimize/map the circuits needs to be specified. We will run combinational equivalence checking and verify the claimed improvements over the current best implementation. If passing all tests, we will publish online the circuit together with the author’s name and affiliation as symbolic recognition. There is no deadline for the submission. The new best results are presented in the International Workshop on Logic & Synthesis (IWLS) each year.
Download:
Please download the benchmarks by cloning the GitHub repository.
git clone https://github.com/lsils/benchmarks.git
Contact:
Please contact us for any questions you might have about the EPFL benchmark suite at [email protected].
Related publications:
[1] Amarú, L., Gaillardon, P. E., & De Micheli, G. (2015). The EPFL combinational benchmark suite. In Proceedings of the 24th International Workshop on Logic & Synthesis (IWLS). (PDF)
[2] ABC Academic synthesis tool: http://www.eecs.berkeley.edu/~alanmi/abc/